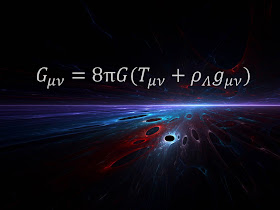Sementara persamaan terkenal tertentu, seperti E = mc2, sangat akrab bagi umum, namun banyak Ilmuwan yang tidak memilih persamaan ini sebagai persamaan favorit mereka. LiveScience menanyai fisikawan, astronom dan matematikawan untuk persamaan favorit mereka; inilah persamaan-persamaan favorit mereka:
Relativitas Umum
Persamaan di atas dirumuskan oleh Einstein sebagai bagian dari teori terobosan relativitas umum pada tahun 1915. Teori ini merevolusi bagaimana para ilmuwan memahami gravitasi dengan menggambarkan gaya sebagai kelengkungan atau warping dari struktur ruang dan waktu.
"Persamaan ini masih menakjubkan bagi saya karena persamaan matematika ini dapat menggambarkan semua tentang apa ruang-waktu itu, " kata astrofisikawan Telescope Science Institute, Mario Livio, yang menominasikan persamaan ini sebagai favoritnya. "Semua kejeniusan Einstein terwujudkan dalam persamaan ini".
"Sisi kanan dari persamaan ini menjelaskan isi energi alam semesta kita (termasuk 'energi gelap ' yang mendorong percepatan kosmik saat ini), " jelas Livio. "Sedangkan sisi kiri menggambarkan geometri ruang-waktu. Kesetaraan mencerminkan fakta bahwa dalam relativitas umum, massa dan energi menentukan geometri, dan secara bersamaan, kelengkungan merupakan manifestasi dari apa yang kita sebut gravitasi."
"Ini adalah persamaan yang sangat elegan," kata Kyle Cranmer, seorang ahli fisika di Universitas New York, menambahkan bahwa persamaan ini mengungkapkan hubungan antara ruang-waktu dan materi serta energi. "Persamaan ini memberitahu Anda bagaimana mereka terkait - bagaimana kehadiran matahari melengkungkan ruang-waktu sehingga Bumi bergerak di sekitar nya dll. persamaan ini juga memberitahu Anda bagaimana alam semesta berevolusi sejak Big Bang dan memprediksi bahwa harus ada lubang hitam."
Model Standar
Model Standar menggambarkan koleksi partikel dasar saat ini yang dianggap membentuk alam semesta kita.
Teori ini dapat dirumuskan dalam persamaan utama yang disebut model standar Lagrangian (diberi nama sesuai dengan nama matematikawan dan astronom Perancis abad ke-18, Joseph Louis Lagrange), yang dipilih oleh fisikawan teoritis Lance Dixon dari SLAC National Accelerator Laboratory di California sebagai rumus favoritnya.
"Formula ini telah berhasil menggambarkan semua partikel dasar dan gaya-gaya yang kita amati di laboratorium sampai saat ini - kecuali gravitasi," kata Dixon. "Dan itu termasuk, tentu saja, partikel-partikel yang baru-baru ini ditemukan Higgs boson, atau phi dalam formula. Ini sepenuhnya konsisten dengan mekanika kuantum dan relativitas khusus . "
Teori Standar Model bagaimanapun, belum bisa bersatu dengan relativitas umum, itulah mengapa teori ini tidak bisa menjelaskan gravitasi.
KALKULUS
Sementara dua persamaan diatas menggambarkan aspek-aspek tertentu dari alam semesta kita, persamaan favorit lain dapat diterapkan untuk segala macam situasi. Teorema dasar kalkulus membentuk tulang punggung dari metode matematika yang dikenal sebagai Calculus, dan menghubungkan dua gagasan utama, konsep turunan dan integral.
"Dengan kata sederhana, Persamaan ini mengatakan bahwa perubahan bersih dari kuantitas yang kurvanya kontinyu dan mulus, seperti jarak tempuh, selama suatu interval waktu tertentu adalah sama dengan integral dari laju perubahan kuantitas itu, yaitu integral dari kecepatan," kata Melkana Brakalova - Trevithick, ketua departemen matematika di Fordham University, yang memilih persamaan ini sebagai favoritnya. "Teorema dasar kalkulus memungkinkan kita untuk menentukan perubahan bersih pada interval berdasarkan laju perubahan atas seluruh Interval . "
Benih-benih kalkulus telah ada sejak zaman kuno, tapi banyak darinya disatukan dalam abad ke-17 oleh Isaac Newton, yang menggunakan kalkulus untuk menggambarkan gerakan planet-planet mengelilingi matahari .
Teorema Pythagoras
Sebuah persamaan tua tapi berguna (oldie but goodie) ini adalah teorema Pythagoras yang terkenal, yang dipelajari setiap siswa pada pelajaran geometri awal.
Rumus ini menjelaskan bagaimana, untuk setiap segitiga siku-siku, kuadrat dari panjang sisi miring c, (sisi terpanjang dari segitiga siku-siku atau sisi yang menghadap sudut siku) sama dengan jumlah dari kuadrat panjang dua sisi lainnya (a dan b). Dengan demikian, a2 + b2 = c2
"Fakta matematika pertama yang membuatku heran adalah teorema Pythagoras," kata matematikawan Daina Taimina dari Cornell University. "Saya masih kecil saat itu dan persamaan ini tampak bagi saya begitu menakjubkan bahwa persamaan ini berlaku dalam geometri dan juga berlaku pada bilangan!"
1 = 0,999999999 ....
Persamaan sederhana ini, yang menyatakan bahwa kuantitas 0,999 ... (dengan angka sembilan yang jumlahnya tak hingga), setara dengan satu, adalah favorit matematikawan Steven Strogatz dari Cornell University.
"Saya suka bagaimana sederhananya persamaan ini - semua orang mengerti apa yang dikatakan persamaan ini - namun persamaan ini juga begitu provokatif," kata Strogatz. "Banyak orang tidak percaya bahwa persamaan ini benar. Persamaan ini juga indah dan seimbang. Sisi kiri merupakan awal matematika, . . Sisi kanan merupakan misteri ketakhinggaan".
Relativitas Khusus
Persamaan Einstein kedua yang masuk dalam daftar ini adalah formula nya untuk relativitas khusus, yang menjelaskan bagaimana waktu dan ruang bukanlah suatu konsep yang absolut, melainkan relatif tergantung pada kecepatan pengamat. Persamaan di atas menunjukkan bagaimana waktu berdilasi, atau melambat, saat semakin cepat laju seseorang.
"Intinya persamaan ini benar-benar sangat sederhana," kata Bill Murray, seorang ahli fisika partikel di laboratorium CERN di Jenewa. "Tidak ada seorang mahasiswa semester awal tidak bisa mengerjakannya, karena tidak ada derivatif yang kompleks dan trace aljabar. Tapi persamaan ini mencakup cara baru dalam memandang dunia, sikap keseluruhan untuk realitas dan hubungan kita dengannya. Tiba-tiba, kosmos yang kaku tak berubah, diganti dengan dunia pribadi, terkait dengan apa yang Anda amati. Murray mengatakan ia lebih suka persamaan relativitas khusus daripada formula yang lebih rumit dalam teori Einstein yang datang kemudian, yaitu relativitas umum. "Saya tidak pernah bisa mengikuti matematika relativitas umum," katanya .
Persamaan Euler
Rumus sederhana ini merangkum sesuatu yang murni tentang sifat bola :
"Persamaan ini mengatakan bahwa jika Anda memotong permukaan bola menjadi sisi-sisi (Faces disingkat F) , tepi (Edges, disingkat E) dan simpul (Vertices, disingkat V), Anda akan selalu mendapatkan V - E + F = 2," kata Colin Adam, seorang matematikawan di Williams College di Massachusetts .
"Jadi, misalnya, kita ambil sebuah tetrahedron, yang terdiri dari empat segitiga, enam tepi dan empat simpul, lalu jika kita meniup keras ke tetrahedron dengan sisi-sisi yang fleksibel, kita bisa bulatkan tetrahedron tersebut menjadi bola. Ini berartii bahwa, bola dapat dipotong menjadi empat sisi, enam tepi dan empat simpul. Dan kita melihat bahwa V - E + F = 2. Ini berlaku juga untuk sebuah piramida dengan lima sisi -empat segitiga dan satu persegi- delapan tepi dan lima simpul. Atau kombinasi lainnya dari sisi, tepi dan simpul," jelas Adam.
"Fakta yang sangat keren! yaitu bahwa kombinatorika dari simpul, tepi dan sisi menangkap sesuatu yang sangat mendasar tentang bentuk bola," kata Adams .
Persamaan Euler-Lagrange dan Teorema Noether
"Ini cukup abstrak, namun luar biasa kuat," kata NYU's Cranmer. "Yang keren adalah bahwa salah satu cara berpikir tentang fisika ini telah bertahan terhadap beberapa revolusi besar dalam fisika, seperti mekanika kuantum, relativitas, dll"
Di sini, L adalah singkatan dari Lagrangian, yang merupakan ukuran dari energi dalam sistem fisik, seperti pegas, tuas atau partikel dasar. " Dengan menyelesaikan persamaan ini, maka kita akan tahu bagaimana sistem akan berkembang seiring waktu," kata Cranmer .
Sebuah spin-off dari persamaan Lagrangian disebut teorema Noether, sebuah teorema yang diberi nama sesuai dengan nama matematikawan Jerman abad ke-20, Emmy Noether. "Teorema ini benar-benar mendasar untuk fisika dan aturan simetri," kata Cranmer. "Secara informal, teorema ini mengatakan bahwa jika sistem anda memiliki simetri, maka akan ada hukum konservasi yang sesuai. Misalnya, gagasan bahwa hukum-hukum dasar fisika adalah sama untuk hari ini ataupun esok (simetri waktu) menyiratkan energi yang kekal. Sedangkan gagasan bahwa hukum fisika adalah sama di sini ataupun di luar angkasa menunjukkan momentum yang kekal. Simetri adalah konsep penting dalam fisika fundamental, terutama karena kontribusi Noether."
Persamaan Callan-Symanzik
"Persamaan Callan-Symanzik adalah persamaan penting dari tahun 1970. Penting untuk menggambarkan bagaimana ekspektasi naif akan gagal dalam dunia kuantum," kata fisikawan teoritis Matt Strassler dari Rutgers University.
Persamaan ini memiliki berbagai aplikasi, termasuk memungkinkan fisikawan untuk memperkirakan massa dan ukuran proton dan neutron, yang membentuk inti atom.
Fisika dasar mengatakan kepada kita bahwa gaya gravitasi, dan gaya listrik, antara dua benda berbanding terbalik dengan kuadrat jarak antara mereka. Pada tingkat sederhana, hal yang sama berlaku untuk gaya nuklir kuat yang mengikat proton dan neutron agar bersama untuk membentuk inti atom, dan yang mengikat kuark bersama-sama untuk membentuk proton dan neutron. Namun, fluktuasi kecil kuantum dapat mengubah ketergantungan gaya pada jarak, yang menyebabkan konsekuensi dramatis bagi gaya nuklir kuat.
"Ini mencegah gaya ini dari penurunan pada jarak jauh, dan menyebabkannya untuk menjebak quark dan menggabungkan mereka untuk membentuk proton dan neutron dari dunia kita," kata Strassler. "Apa yang persamaan Callan-Symanzik lakukan adalah menghubungkan efek dramatis dan sulit untuk dihitung ini, yang penting saat jarak kira-kira seukuran proton, ke efek yang lebih halus namun mudah untuk dihitung yang dapat diukur ketika jarak jauh lebih kecil dari proton . "
Persamaan Permukaan Minimal
"Persamaan permukaan minimal entah bagaimana mengkodekan film sabun yang indah yang terbentuk pada batas kawat ketika Anda celupkan ke dalam air sabun," kata matematikawan Frank Morgan dari Williams College. "Fakta bahwa persamaan ini adalah 'nonlinier,' yang melibatkan gaya dan produk derivatif, adalah petunjuk matematika kode untuk perilaku mengejutkan dari film sabun. Hal ini berbeda dengan persamaan linear yang lebih akrab, yaitu diferensial parsial, seperti persamaan panas, persamaan gelombang dan persamaan Schrödinger fisika kuantum."
BONUS
Baca Juga:
Source: LiveScience